
We thank the Austrian Science Fund (FWF) for support (10.55776/PAT2839723). Funded by the European Union - NextGenerationEU. Click here for the FWF description.
Popular summary -- scientific details below: Quantum theory promises technological applications that would be impossible within classical physics: faster computation, more accurate metrology, or the generation of provably secure random numbers. However, to make this work, we first need to test whether our devices are really quantum and work as desired -- a task called certification. This is not only relevant for technology, but also for fundamental physics: given some large physical system, such as a Bose-Einstein condensate, how can we prove that its properties cannot be explained by classical physics? In other words, how can we certify its nonclassicality?
In this project, we will develop a new method to do so, both theoretically (via mathematical proofs and conceptual argumentation) and experimentally (with concrete data supplied by colleagues at ETH Zurich). Our approach is based on the phenomenon of contextuality: properties of quantum systems cannot be independent of the choice of implementation of the measurement procedures. In other words, if we ask Nature a question, then the answer must sometimes depend on the experimental context. Here, we develop methods that allow us to certify this phenomenon in physical systems even if they are very large and can only be probed in coarse and incomplete ways, and even if we know nothing about their composition, time evolution, or the physical theory that describes them.
Our project will improve upon earlier work in several respects. Most earlier attempts to certify nonclassicality in large quantum systems have relied on the notion of Bell nonlocality: correlations between several particles cannot be explained by any local hidden-variable model. However, this has only been possible under strong additional assumptions, since it is impossible to measure all particles of a large quantum system individually. Moreover, both the experimental detection as well as the theoretical definition of contextuality (in the sense that is relevant for our project) has been restricted to situations in which the experimenter can measure all properties of the physical system completely and exhaustively (tomographic completeness). In our project, we will drop these assumptions and develop methods that are device- and theory-independent and that work with coarse and incomplete experimental data.
Our projects spans quantum physics from its philosophical foundations up to its experimental implementation. Conceptually, we will shed light on the question of how coarse experimental data can render a microscopic theory implausible. Mathematically, we will develop methods that can certify this notion of contextuality with algorithms and inequalities. Finally, we will apply our results to concrete experimental data from nanomechanical oscillators and Bose-Einstein condensates.
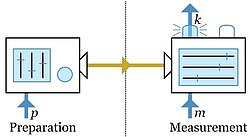
Spekkens' notion of generalized noncontextuality
Under what conditions can we say that a physical system defies classical explanation? Spekkens' notion of generalized contextuality [1] is arguably our currently best candidate for answering this question, in particular in all cases where we consider single physical systems without any causally relevant differentiation into subsystems (as in Bell's theorem). In contrast to the Kochen-Specker version, generalized noncontextuality (GNC) does not rely on the assumptions that measurements are projective or noiseless, and it does not even rely on the validity of quantum theory. GNC can be experimentally refuted in robust ways (for example, via GNC inequalities), it can be conceptually grounded on Leibniz's Principle of the Identitity of the Indescernibles, and it can be mathematically understood as the demand that the linearity structure in the operational (laboratory) theory should be consistent with the linearity structure in its hypothetical underlying "classical" hidden-variable model.
It is a mathematically and conceptually compelling concept. However, due to its reliance on Leibniz's Principle, its range of applicability was hitherto restricted to situations where we assume "tomographic completeness": that our experiment probes a given physical system completely. The goal of our project is to extend its range to experiments where this assumption is not satisfied. This involves many experiments of interest, in particular, experiments on "large" quantum systems (such as Bose-Einstein condensates) that admit only a partial probing of its degrees of freedom (say, only measurements of collective degrees of freedom).
A new perspective and a generalization of generalized noncontextuality
In our paper [2], we have suggested a different perspective on GNC that circumvents this problem in some sense. That is, instead of seeing GNC as a condition about physical reality (and whether it can be classical in a way that respects Leibniz's Principle), we see it as a methodological principle that tells us under what conditions a hypothetical fundamental theory could be a plausible explanation of an effective theory (describing e.g. the laboratory data): Processes that are statistically indistinguishable in an effective theory should not require explanation by multiple distinguishable processes in a more fundamental theory. For prepare-and-measure scenarios as depicted above, this condition boils down to the mathematical constraint that the effective probabilistic theory should admit of a linear embedding into the fundamental probabilistic theory.
In the special case where the fundamental theory is assumed to be classical (i.e. describable by classical probability theory), this reduces to Spekkens' version of GNC (exactly in its mathematical formulation, even if not in its intended conceptual interpretation). But we obtain a broader and more powerful notion: we can also ask, for example, whether our effective laboratory data has a plausible description in terms of quantum theory. This should allow us to design novel experimental tests of quantum theory, and this is one of several research directions that we are pursuing in this project.
Project goals
Our project involves conceptual ("philosophical"), mathematical and experimental aspects.
Conceptually, we will analyze in more detail under what conditions coarse experimental data can certify the implausibility of a more fundamental underlying classical description. Since Leibniz's Principle is silent about this scenario, we have to refer to "no-finetuning" principles or "typicality" arguments that are often invoked in the context of thermodynamics. Some of this will be done in collaboration with our colleagues at ICTQT Gdańsk.
Mathematically, we will analyze how contextuality can be inferred from coarse experimental data under additional assumptions (such symmetries of the experimental setup or spatiotemporal constraints). We will extend "theory-agnostic tomography" [3] to systems in which tomographic completeness is dropped, and we will implement methods to test for the quantum embeddability of the resulting generalized probabilistic theories.
Experimentally, we will apply our insights to concrete physical systems, including Bose-Einstein condensates and mechanical resonators. This will be done in collaboration with Matteo Fadel (ETH Zurich).
References
[1] R. W. Spekkens, Contextuality for Preparations, Transformations, and Unsharp Measurements, Phys. Rev. A 71, 052108 (2005).
[2] M. P. Müller and A. J. P. Garner, Testing Quantum Theory by Generalizing Noncontextuality, Phys. Rev. X 13, 041001 (2023). DOI:10.1103/PhysRevX.13.041001.
[3] M. D. Mazurek, M. F. Pusey, K. J. Resch, and R. W. Spekkens, Experimentally Bounding Deviations From Quantum Theory in the Landscape of Generalized Probabilistic Theories, PRX Quantum 2, 020302 (2021).
Müller Group

Markus Müller
Group Leader+43 (1) 51581 - 9530

Manuel Mekonnen
PhD Student




