

We are grateful to the Austrian Science Fund FWF via Quantum Science Austria for funding our project "Local Operations on Quantum Fields" (jointly with Časlav Brukner, Borivoje Dakić, and Miguel Navascués).
The description below is about our group's part in this project, involving PhD student Manuel Mekonnen and PI Markus Müller. It also describes our group's earlier work on Quantum Reference Frames, which is closely related to this project.
"Internal" quantum reference frames (QRFs)
Recently, there has been a wave of interest in an internal notion of quantum reference frames; see the Brukner group pages for a description. How can we describe the state of a quantum system "relative to one of its subsystems"? For example, if we believe that there is no absolute time, then we should describe time evolution relative to a quantum subsystem of the universe that serves as a clock. How can this be done, and how can we "switch" between different such reference frames?
In our group, we are interested in the mathematical and conceptual foundations of QRFs. To this end, we have worked out a detailed study of QRFs for finite Abelian groups, which can be thought of as a discretization of spatial translations [4,5]. This describes a case that can be treated with full mathematical rigor and simplicity, demonstrating how and to what extent the "perspective-neutral" and "Vienna" approaches to QRFs are equivalent, and why. This case is already interesting enough to cover several physically relevant examples such as the "paradox of the third particle" [10], which we have rigorously analyzed and arguably solved with a careful algebraic treatment of composition under symmetries [4]. In a nutshell, we show that the way that "two particles are embedded into three particles" is a priori undefined without further operational specification. This has important consequences for the notions of subsystem, locality and causality under global symmetries, which will also be part of our quantA project. Our work also considers the question of what happens to the quantum information contained in a state under these symmetry transformations -- that is, if the system in question is entangled with an ancilla system.
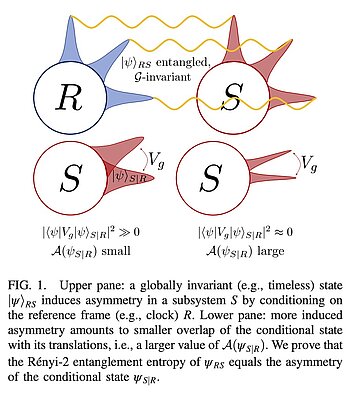
We have also contributed to the generalization of the perspective-neutral approach to arbitrary symmetry groups [6]. Furthermore, we have analyzed the Page-Wootters mechanism in the case of imperfect clocks. This mechanism replaces background time by quantum correlations with a clock. We have proven that the amount of entanglement with the clock tells us exactly how much time asymmetry is induced in the system, and this holds more generally for arbitrary symmetries and QRFs in the perspective-neutral approach. This gives a quantitative realization of the slogan "time from quantum correlations".
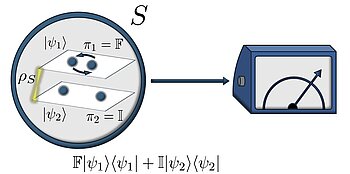
Symmetries and locality
In this quantA project, we will be interested in the different notions of locality as they arise in quantum mechanics, gauge theories, quantum field theory, and ultimately quantum gravity. Our starting point will be the notion of subsystem composition described above, with work on QRFs indicating that composition and marginalization are not as straightforward under global quantum symmetries as they would be under "classical" ones.
In particular, we will be concerned with questions such as: how is the notion of locality encoded into the structure of subalgebras or operator systems? How is locality built into the notion of gauge theories, and what distinguishes global from local gauge symmetries? Is there a difference between the classical and quantum scenarios? Our research will span quantum information, device-independent quantum foundations, and operator-algebraic methods to improve our understanding of how locality is woven into the fabric of physics.
An important step to do this is to understand the perspective-neutral framework for the case that a QRF is not necessarily a (tensor product) subsystem. Recently (as of 2025), we have applied this generalization to the case of indistinguishable particles, where the QRF terminology turns out to be of great use: it allows a particularly elegant and conceptually transparent treatment of entanglement of Bosons or Fermions. Furthermore, we have shown that it allows us to understand why nature does not admit more general statistics than Bosonic or Fermionic [8], called parastatistics: traditional permutation invariance (which allows parastatistics) can be seen as invariance under a change of a classical "frame of labelling"; the corresponding quantum version, i.e. invariance under a change of quantum frames of labelling ("quantum permutations", see figure), turns out to rule out parastastistics. This demonstrates the explanatory power, but also subtle restrictions of recently proposed quantum covariance principles [9].
References
[1] F. Giacomini, E. Castro-Ruiz, and Č. Brukner, Quantum mechanics and the covariance of physical laws in quantum reference frames, Nat. Commun. 10, 494 (2019).
[2] A. Vanrietvelde, P. A. Höhn, F. Giacomini, and E. Castro-Ruiz, A change of perspective: switching quantum reference frames via a perspective-neutral framework, Quantum 4, 225 (2020).
[3] L. Loveridge, P. Busch, and T. Miyadera, Relativity of quantum states and observables, EPL 117, 40004 (2017).
[4] M. Krumm, P. A. Höhn, and M. P. Müller, Quantum reference frame transformations as symmetries and the paradox of the third particle, Quantum 5, 530 (2021). DOI:10.22331/q-2021-08-27-530.
[5] P. A. Höhn, M. Krumm, and M. P. Müller, Internal quantum reference frames for finite Abelian groups, J. Math. Phys. 63, 112207 (2022). DOI:10.1063/5.0088485; arXiv:2107.07545.
[6] A. de la Hamette, T. D. Galley, P. A. Höhn, L. Loveridge, and M. P. Müller, Perspective-neutral approach to quantum frame covariance for general symmetry groups, arXiv:2110.13824.
[7] A. de la Hamette, S. L. Ludescher, and M. P. Müller, Entanglement-Asymmetry Correspondence for Internal Quantum Reference Frames, Phys. Rev. Lett. 129, 260404 (2022). DOI:10.1103/PhysRevLett.129.260404; arXiv:2112.00046.
[8] M. Mekonnen, T. D. Galley, and M. P. Müller, Invariance under quantum permutations rules out parastatistics, arXiv:2502.17576.
[9] A. de la Hamette, V. Kabel, E. Castro-Ruiz, and Č. Brukner, Quantum reference frames for an indefinite metric, Commun. Phys. 6, 231 (2023).
[10] R. M. Angelo, N. Brunner, S. Popescu, A. J. Short, and P. Skrzypczyk, Physics within a quantum reference frame, J. Phys. A: Math. Theor. 44, 145304 (2011).
[11] D. N. Page and W. K. Wootters, Evolution without evolution: Dynamics described by stationary observables, Phys. Rev. D 27, 2885 (1983).








